|
Galderak
-
Aukeratu Zenbaki angeluzuzena pantailaren beheko aldean. Mugitu goiko irristailua eta begiratu zelan sortzen diren zenbaki angeluzuzenak. Egin gauza bera, orain, astiro, eta bete honako taula honen bigarren zutabea:
| n |
Angeluzuzena |
Triangeluarra |
Karratua |
Pentagonala |
Hexagonala |
| 1 |
|
|
|
|
|
| 2 |
|
|
|
|
|
| 3 |
|
|
|
|
|
| 4 |
|
|
|
|
|
| 5 |
|
|
|
|
|
| 6 |
|
|
|
|
|
| 7 |
|
|
|
|
|
| 8 |
|
|
|
|
|
| 9 |
|
|
|
|
|
| 10 |
|
|
|
|
|
-
Laukizuzen bakoitzaren neurritzat luzetara zein zabaletara duen zirkulu kopurua hartzen badugu, zer neurri ditu 1. zenbaki angeluzuzenari dagokion laukizuzenak? Eta 2. zenbaki angeluzuenari dagokionak? Eta 3.ari dagokionak? Eta 10.arenak? Eta 100. zenbaki angeluzuzenari dagokionak? Zelan kalkulatuko zenuke zenbaki angeluzuzena, dagokion laukizuzenaren neurrietatik abiatuta?
-
Zein dira n. laukizuzenaren neurriak? Zenbat zirkuluk osatzen dute? Zer formula erabil dezakegu n. zenbaki angeluzuzena (R(n)) kalkulatzeko? Osatu:
R(n) = ……
-
Desaktibatu Zenbaki angeluzuzena dakarren laukitxoa, eta aktibatu Zenbaki triangeluarra dakarrena. Mugitu goiko irristailua, eta behatu zelan sortzen diren zenbaki triangeluarrak. Mugitu berriro, baina astiro, eta osatu 1. galderako taulako 3. zutabea (Triangeluarra).
-
Erkatu 2. eta 3. zutabeetako zenbakiak. Zer erlazio dago euren artean?
-
Interpreta dezagun geometrikoki aurreko erlazioa. Aktibatu aldi berean Zenbaki angeluzuzena eta Zenbaki triangeluarra laukitxoak. Mugitu goiko irristailua. Ikusten ari zarena bat dator taulan aurkitu duzun erlazioarekin?
-
Aurreko erlazioa kontuan izanik, zer formula erabiliko zenuke n. zenbaki triangeluarra (T(n)) bilatzeko? Osatu:
T(n) = ……
-
Zenbaki triangeluarra lortzeko beste modu bat da errenkada bakoitzeko zirkulu kopuruak batzea. Zenbaki triangeluarrei goitik behera begiratzen badiezu, zern baturak emango liguke 2. zenbaki triangeluarra? Eta 3.a? Eta 4.a? Eta 10.a? Eta 100.a?
-
Zelan kalkula daiteke lehenengo n zenbaki arrunten arteko batura? Osatu:
1 + 2 + 3 + 4 + 5 + .... + n = ……
-
Egin klik  botoian, hasierako baldintzetara itzultzeko. Aktibatu Zenbaki karratua laukitxoa. Mugitu goiko irristailua, eta begiratu zelan sortzen diren zenbaki karratuak. Mugitu, berriro, baina astiro, eta osatu 1. galderako taulako 4. zutabea (Karratua).
-
Aurkitu n. zenbaki karratua (C(n)) emango digun formula. Osatu:
C(n) = ……
-
Egia da honako erlazio hau: R(n) = C(n) + n? Egiaztatu taulako balioekin zein grafikoki. (Aktibatu aldi berean Zenbaki angeluzuzena eta Zenbaki karratua laukitxoak).
-
Egin klik botoian hasierako baldintzetara itzultzeko, eta aktibatu aldi berean Zenbaki triangeluarra eta Zenbaki karratua laukitxoak. Mugitu goian eta ezkerrean dagoen irristailua. Ba al dago erlaziorik zenbaki karratuen eta triangeluarren artean? Egiaztatu taulan aurkitu duzun erlazioa. Zelan idatziko zenuke aljebraikoki?
-
Egin klik botoian hasierako baldintzetara itzultzeko, eta aktibatu Zenbaki pentagonala. Mugitu goiko irristailua eta begiratu zelan sortzen diren zenbaki pentagonalak. Mugitu, berriz, baina astiro, eta osatu 1. galderako taulako 5. zutabea (Pentagonala).
-
13. galderan, zenbaki karratu bat bi zenbaki triangeluarren batura legez jartzeko modua aurkitu dugu. Jarri al izango dugu zenbaki pentagonal bat zenbaki triangeluarren batura gisa? Begiratu honako irudi honi, eta ahalegindu geometrikoki adierazitakoa balio-taulan interpretatzen.
-
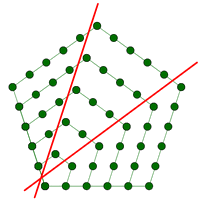
Zer formulak emango liguke n. zenbaki pentagonala (P(n)) aurreko atalean aurkitutako erlazioren batetik edo taulan aurki dezakezun beste batzuetatik abiatuta? Osatu:
P(n) = ……
-
Egin klik botoian hasierako baldintzetara joateko, eta aktibatu Zenbaki hexagonala laukitxoa. Mugitu goiko irristailua, eta begiratu zenbaki hexagonalen sorkuntza. Mugitu, berriz, baina astiro, eta osatu 1. galderako taulako 6. zutabea (Hexagonala).
-
Aztertu taula. Aurkitu erlazioren bat zenbaki triangeluarren eta hexagonalen artean. Zelan adieraziko zenuke? Zer interpretazio geometriko emango zenuke? Irudikatu eskematikoki 5. ordenako zenbaki hexagonal bat.
-
Aurkitu formula bat, n. zenbaki hexagonala (H(n)) emateko balioko duena, aurreko ataleko erlazioren batetik abiatuta edota taulan aurki ditzakezun beste batzuetatik abiatuta. Osatu:
H(n) = ……
-
Bilatu beste erlazio batzuk taulan. Idatzi bakoitza aljebraikoki, eta interpretatu geometrikoki.
-
Egin klik botoian hasierako baldintzetara itzultzeko, eta aktibatu Beste zenbaki poligonalak laukitxoa. Orain, beste irristailu bat duzu pantailaren azpiko aldean, poligonoaren alde kopurua zehazteko; eta, lehengo irristailuarekin konbinatuz, 12. ordenarainoko zenbaki poligonalak osa ditzakezu. Gehitu zutabe gehiago zeure taulan 7, 8, … ordenako zenbaki poligonalak eratzeko. Bete zutabe berriak irristailuen laguntzarekin. Egiazta ditzakezu emaitzak Erakutsi balio-taula laukitxoa aktibatuz.
Aurreko ataletan, zenbaki karratuak, pentagonalak eta hexagonalak zenbaki triangeluarren funtzio gisa idatzi ahal izan dituzu. Zenbaki triangeluarrak oinarri ona dira gainerako zenbaki poligonalak kalkulatzeko. Edozein zenbaki poligonal jar daiteke zenbaki triangeluarren funtzio gisa? Honako galdera honi erantzutea izango da, orain, zure helburua: ediren formula bat zenbaki poligonal bat zenbaki triangeluarren konbinazio gisa idazteko. Zehatzako esanda, n. zenbaki poligonala idatzi behar duzu zenbaki triangeluarren eta poligonoaren alde kopuruaren (p) funtzio gisa.
-
Azken erronka: aurreko atalean, zenbaki poligonal bat zenbaki triangeluarren funtzio gisa idatzi ahal izan duzu. Gai izango zinateke formula hori poligonoaren alde kopuruaren (p) eta zenbaki poligonalak hartzen duen lekuaren (n) funtzio gisa idazteko?
|
